みをつくしのひとりよがり

2022/08/10にブログ名を変えました．仕事や生活に役立ちそうな（実際に役立つかは別として）数学・物理ネタをつらつらと書いていこうと思ってます．

近似値問題～ニュートン法～

Math

前々回，前回と，a^bと b^aの大小関係を調べました．その中で，a \neq bでも a^b = b^aとなるときがあることがわかりました．そして，その aと bの関係式を b = \theta(a)としてグラフを描きました．
ここでは， b = \theta(a)のグラフの描き方を書いていきます．

ニュートン法

これは高校数学の範囲でも書かれるような比較的簡単なものです．以下，少しつらつらと書いていきます．

方程式： f(x) = 0の実数解の「近似値(真の解に近い数値)」を x = x_0とします．
「真の解」はグラフ： y = f(x)と x軸との交点として与えられますが， x = x_0は近似値なので x軸上にはありません．そこで，その点における y = f(x)の接線を引いてみます．
　 y - f(x_0) = f'(x_0)(x - x_0)

この接線と x軸の交点を (x_1, 0)とすると，
　 \begin{align} 0 - f(x_0) &= f'(x_0) (x_1 - x_0) \\ x_1 &= x_0 - \frac{f(x_0)}{f'(x_0)} \end{align}

点 (x_1, f(x_1))が点 (x_0, f(x_0))よりも真の解に近づいているとは限らないですが，これを繰り返していくと，真の解に近づくようになります．*1つまり，
　 \displaystyle{ x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)} }

という漸化式を使って，どんどん真の解に近づけていくこと(数値解を得ること)を考える．これがニュートン法と呼ばれる方法になります．*2


実際に数値解を求めるとき， f'(x)という微分をわざわざ計算するのも，何かと面倒だったりします．そこで，
　 \displaystyle{ f'(x_n) \rightarrow \frac{f(x_n + h) - f(x_n - h)}{2h} }

と置き換えてあげると， f(x)という一つの関数へ数値代入を繰り返すだけで近似解を求めることができます．「微分係数」の問題として，こういう変形が出てきますよね．
このようにしたときに，「初期の近似値」以外に必要となるパラメータは，

  • 微分係数の代わりとなる式における「幅」： hの大きさ
  • 漸化式をくり返し使う回数の上限：N(ある程度の回数くり返せば、もうエエでしょという回数)
  • 漸化式を用いる前と後の数値の差： |x_{n+1} - x_n|の上限(差がその値よりも小さくなるまではくり返す、それ以上はもう差は縮まらないでしょうという限界)

となります．

b = \theta(a)の描き方

以下のような手順を踏んで，グラフを描いています．

  1. グラフの始点と終点となる aの値の範囲を与えます．( a_0 \leqq a \leqq a_Mの範囲でグラフを描く)
  2. この区間を \delta = 0.01に区切り， \displaystyle{ a_i = a_0 + {\delta} \cdot i \ \ \left(0 \leqq i \leqq M, \ M = \frac{a_M - a_0}{\delta} \right) }としました．*3
  3. それぞれの a_iについて，ニュートン法(上で書いた微分を置き換えた式を用いた方法)で，近似解を得ます．
  4. それらを連ねたものが，グラフとなって現れてきます．


ニュートン法の計算では，上に書いた「幅」や「くり返しの上限」を与えることになります．このように書くと，比較的簡単な感じに見えますが，実はそうではありません．

上記の 3.を実行するとき，「幅」などのパラメータよりももっと大事な「初期の近似値」というものが必要になります．いまの問題では，「自明な解」が存在するため，この解に引きずられないような近似値を与えなければなりません．特に， b = aとの交点となる点 (e,e)近辺では，それがシビアになってきます．
で，どのようにしたのかというと，ちょっとインチキじみた方法を使いました...

3.1. a = 2.00, \ 2.05, \ 2.10, \ \ldots , \ 2,70, \ 2.71, \ 2.72, \ e という値のそれぞれに対して， \displaystyle{ y = x - \frac{a}{\log a} \cdot \log x} のグラフと x軸との交点の座標を読み取り，座標面上にプロットします．
3.2. その点列を「通る」ような曲線を探します．ここでは， \displaystyle{ g(a) \approx \frac{c_1}{a} + \frac{c_3}{a^3} + \frac{c_5}{a^5} + c_0 }という関数を考えました．*4
3.3. a = a_iとして g(a_i)を計算し，それぞれの近似値として与えることで，正しい(欲しい方の)解を得ることにしました．

たとえば，上の関数を \displaystyle{ g(a) \approx \frac{c_1}{a} + \frac{c_3}{a^3} + \frac{c_5}{a^{\color{red}{4}}} + c_0 }のように，5乗→4乗と間違うだけで a = eの近傍で自明な解に引きずられた結果がでてしまいます(下図)．

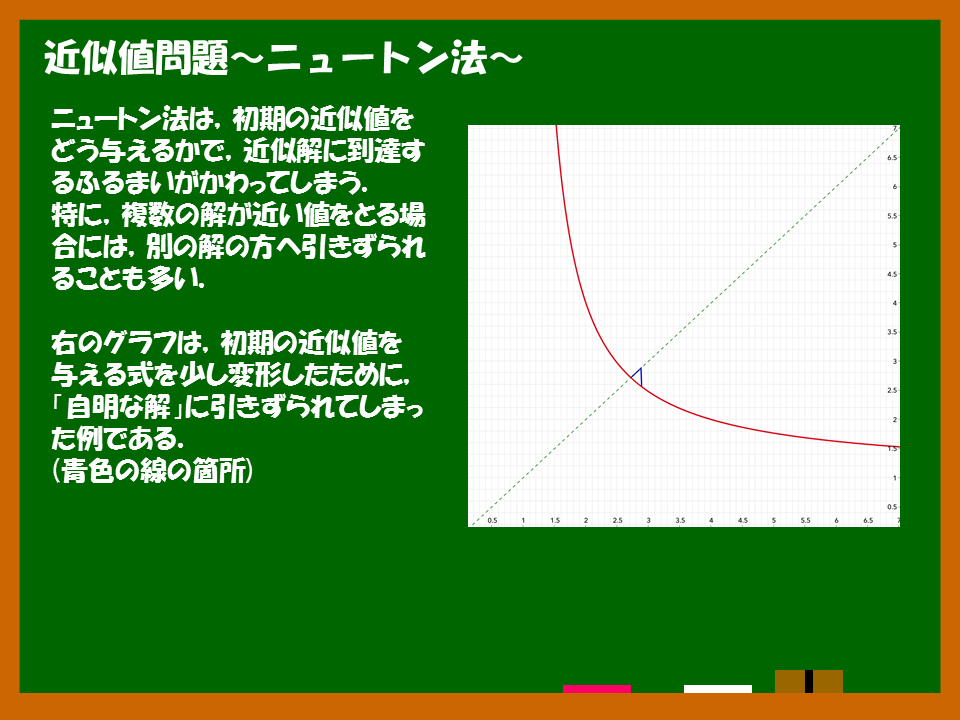
この初期の近似値を与える式を探すのが，一番面倒だったかもしれません．その式自体も比較的精度の高い近似解だとも言えるのですが， 1 < a < 2や 4 < aの範囲ではズレてきます．でも，自明な解よりははるかに近くに存在するので，正しく収束してくれました．

ニュートン法は一見ややこしそうに見えるのですが，ここでは記さなかったものの図形的なイメージで理解しやすい内容だと思うので，一度手を動かして確認してみることをお奨めします．

*1:極値の近くなどでは，期待どおりの解に到達できない場合もあります．

*2:たとえば， f(x) = x^3 - 2xという整式に対して漸化式は， \displaystyle{ x_{n+1} = \frac{2 {x_n}^3}{3 {x_n}^2 - 2} }となります．この数列の極限値を \chiと置いて，x_{n+1}と x_nをそれぞれ置き換えてみると， \displaystyle{ \chi = \frac{2 \chi^3}{3 \chi^2 - 2}, \ \chi^3 - 2 \chi = 0 }となって，元の方程式の解に収束するんだなあということが見えてきます．

*3:Mが自然数となるよう，a_0や a_Mは，小数第1位程度の値を指定しています．

*4:反比例の形っぽいなあというところから，補正項を追加するイメージで，この形に行き着きました．このように関数形を与えることで，その係数を算出してくれるようなソフトウエアが簡単に手に入ります．便利ですね．それぞれの係数は， c_1 = 3.8776, \ c_3 = 5.0832, \ c_5 = 15.688, \ c_0 = 0.9341となりました．