先日熱気球の問題 を取り上げましたが、いい応用問題があったので取り上げることにします。気体分子運動論を除けば、この問題で一通り熱力学は学習できるような気がします。元ネタは、2006年京都大学前期物理第3問です。
※分数や指数の式が頻繁に現れるので、数式については TeXを用いて画像として貼り付けています。
小問(1):ある高度における大気の圧力と密度

冒頭に登場する断熱変化における圧力と体積の関係は、ポアソンの式*1と呼ばれるものです。参考書などにはちょくちょく登場してくる式です。は比熱比であり、
(
:定圧モル比熱、
:定積モル比熱)として表されます。
地表における大気の圧力:は、状態方程式から導きます。分母・分子にモル質量(分子量)をかけることで密度を導いています。

これが【あ】の答になります。
ある高度における大気について、圧力は上のポアソンの式と状態方程式から導きます。であることにも注意しながら計算を進めます。

これが【い】の答となります。
密度については、以前にも説明したボイル・シャルルの法則もどきの式から導きます。

これが【う】の答となります。
「同じ高度での内(気球内)・外(大気)の話」と「異なる高度での大気の話」とを混同しないように整理することが、この問題を解くカギになります。
小問(2):とりあえず、地表で気球を浮上させる

体積ゼロからスタートしているところが、ちょっと憎いところです。しかし、立てる式は前回の説明と同じです。体積:まで空気を入れたところで浮かび始めたとすると、
(浮力)=
(気球内の空気の質量による重力)=
(気球の質量による重力)=
気球内の空気の密度:については、【う】で考えた式において
とすることで
と求められるので、

これが【え】の答となります。
密度が ρ1の気体の質量は ρ1・Vですから、モル数:N【お】は
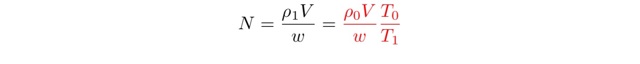
次の【か】【き】は、熱力学の第1法則と内部エネルギーを用いて求めます。内部エネルギー【き】は、定積モル比熱を用いて

あとは、(外部にした仕事)が求まれば、
(与えた熱量)が求められます。「気球の下部が開いた状態」なので、定圧変化であることを考慮して、

よって、与えられた熱量:【か】は、

この熱量は、定圧モル比熱と定積モル比熱の間に成り立つ関係式:というマイヤーの関係式を知っていると、すぐに求められてしまいます。この関係式を知っていると、
より、先に出てきた比熱比:
が 1より大きいことも示すことができます。
小問(3):大空へ飛び出す気球

「気球内の空気の温度と体積が変化しない」ということは、気球内の空気の質量(=密度×体積)は変化しないということです。そして、「静止した」とは力がつり合っているということを表しています。この高度における大気の圧力は【い】、密度は【う】で求めたものを使います。
ここでも「大気の密度、温度」と「気球内の密度、温度」を混同しないように整理できるかがポイントです。大気は閉じていない系であり、気球内は閉じた系です。
(浮力)=
(気球内の空気の質量による重力)=
(気球の質量による重力)=
にそれぞれの値を代入して、

これが【く】の答となります。
「気球の下部を開いた(気球内の圧力は大気と同じになる)」とき、高度が変わらなかったということは、力のつり合い関係が保たれていたことになります。ということは、気球内の空気の質量は変わらなかったということになります(浮力や気球の質量は変化しておらず、力のつり合いの関係自体は成立したままだから)。すなわち、空気の出入りはなかったことになります。ここがポイントです。空気の出入りがないということは「閉じた系」です。よって、ボイル・シャルルの法則を用いて、

これが【け】の答になります。
最後に、と
の大小関係を求めます。これは【け】の結果から

であり、ですから、( )内が 1より大きいか小さいかがわかればよいことになります。そこで、小問(2)の過程を思い出すと、
- 温度:
の気体を体積:
まで入れた時点で浮き上がり、
- さらに、体積:
になるまで、その気体を入れた。
ということなので、力のつり合い関係は、【え】で立てた式の等号成立以降の話なので、

よって、となり、(2) T1より低い【こ】となります。
小問(3)の最後がちょっと気持ち悪い感じになりますが、結果論的に言えば次のようになります。
- 気球の下部を開く前、気球内の圧力は大気よりも高かった(
より)。
- このまま開けば、圧力の低い方へ気体は出ていくはず、
- しかし、気球内の温度を下げることで、気球の体積を保ちつつ、気体の流出も防いだ。
- 体積が保たれたことで得られる浮力も変わらず、そのまま高度も保たれた。
一言で「高度を保つように温度を操作した」と言った方がわかりやすいような気もします。
*1:導出については,大気の物理~その3(2年越し)~ - 理系男子の独り善がりに記しています。