先日のボブスレーの話 の中で,ちょこっと言葉として出したものです.ちょっと難しい言葉ですが,大事なことなので少し書いてみたいと思います.「次元」というと,相対性理論で出 てくる「4次元」,超弦理論で出てくる「26次元」,そしてルパンの相棒(これが一番多いでしょうね)といったものを想像する人が多いと思います.
意外な厄介者
物理を勉強する上で意外な厄介者があります.それは「単位系」と呼ばれるものです.これは物理量を表す基本単位の組合せのことで,「MKSA単位系」や「CGS単位系」というものがあります.
- MKSA単位系:M(メートル),K(キログラム),s(秒),A(アンペア)を基本単位とする
- CGS単位系:cm(センチメートル),g(グラム),s(秒)を基本単位とする
た とえば,「1キログラム」という表現は MKSA単位系での表現であり,CGS単位系では「1000グラム」と表すことになります.そもそも単位自体,人間が勝手に決めたものとも言えるわけで, 質量なら質量,長さなら長さ・・・として扱えるものを考えようというのが「次元」の考え方になります.
次元の定義
ある物理量:Aに対して,Aの次元を以下のように定義します.

[L]は長さ,[M]は重さ,[T]は時間,[I]は電流,それぞれの基本単位を表し,x, y, z, wをそれぞれの単位の次元と呼びます.以下,例として,速さ:v,運動量:p,力:F,エネルギー:Eの次元を表すと,
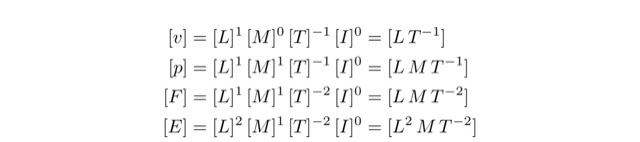
式で書くと難しそうに見えますが,少し噛み砕いた表現をすれば
- 速さ:vは,距離÷時間
- 運動量:pは,質量×速さ
- 力:Fは,質量×加速度=質量×速さ÷時間
- エネルギー:Eは,質量×(速さ)^2 または 質量×加速度×高さ
ということを表しているだけです.このように言葉を用いた式が,次元のイメージに一番近いかもしれませんね.
エネルギーの次元については,運動エネルギーの式を考えているか,位置エネルギーの式を考えているかの違いになります.しかし,エネルギーの次元は同じになります.当然のことですが,同じ次元同士の物理量でないと,足し合わせたり,差し引いたりといったことはできません.
同じ次元同士を考える例
上の例では電流の次元が出てきませんでした.ここでは,その電流の次元を用いたものを考えてみます.フレミングの左手の法則により,磁界中の電流が受ける力の大きさは
B×I×L× sin θ (B:磁束密度,I:電流の大きさ,L:磁界中の電流が流れる部分の長さ,θ:磁界の方向と電流の方向がなす角)
として表されます.ここで sin θは次元を持たない量であり,このようなものを「無次元である」といいます.上の例で力の次元は [LMT^(-2)]と確認しているので,
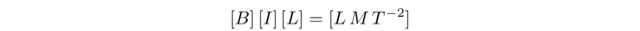
という式が成り立ちます.これより,磁束密度と磁束:Hの次元を調べると,
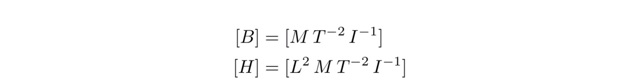
で あることが導かれます.電磁気の問題を考えていると,時間の要素は感じられないと思います.しかし,次元の中にはしっかりと時間の次元が現れています.こ れは,たとえば電流自体が銅線中を流れる自由電子の速さから考えていたりすることに起因しています.このように,次元は物理量の本質を表してくれるように なるのです.
次元解析
次元を比較するということを応用すると,「なんか因果関係がありそう」というものの関係を明らかにできることがあります.その例を挙げてみます.
音の高さは,その音の周波数の大きさにより決まります.たとえば,ギターでは
- 弦の長さ(指を押さえる位置):S
- 弦にはたらく張力(「ペグ」と呼ばれる金具により張りの強さを変える):T
- 弦の太さ(線密度):ρ
によって決まります.そこで,周波数:fが kを比例定数として
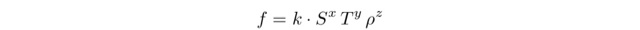
と表されるとして,x, y, zがどうなるかを考えます.[f]=[T^(-1)]なので,
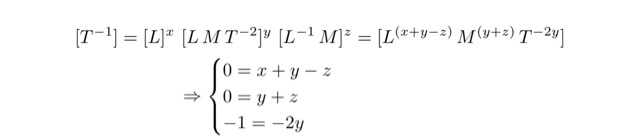
のように指数に対する連立方程式が導かれ,x= -1, y= 1/2, z= -1/2という解を得ます.結果,

と 表されることがわかります.このように次元を用いて関係を調べることを次元解析と言います.この例では,連立方程式の解が得られた結果,kは無次元の比例定数となります.しかし,場合によっては,比例定数も次元をもつ場合があります.たとえば,万有引力の式における比例定数である万有引力定数は次元をもっています(ここでは詳細は書きません,ご自分で調べてみてください).
導出された式に対して,このような見方ができるようになると,その式が表している物理現象の理解にもつながると思います.無理に次元を用いなくとも,通常の単位でもある程度の理解はできると思います.
最後に,次元解析を用いれば,センタ試験のような選択肢問題で異なる次元をもつ選択肢は外すといったワザも使えるようになります.ただ,最近の問題はどの選択肢も次元は合わせられていますね(苦笑).