第2問は,微積を使う「計算問題」という感じですね.こちらはABまとめて,ポイントになりそうなところだけ書いてみます.
A:湖底にある生物の卵を駆除する
Aは指示に従って計算をしていくだけなので,特にこれ!という重要なポイントはないかと思います.強いて言えば,(A-4)で出てくる積分の計算ぐらいでしょうか?ややこしい定数項は,一度別の文字で置き換えて計算するといった工夫をした方がいいですね.
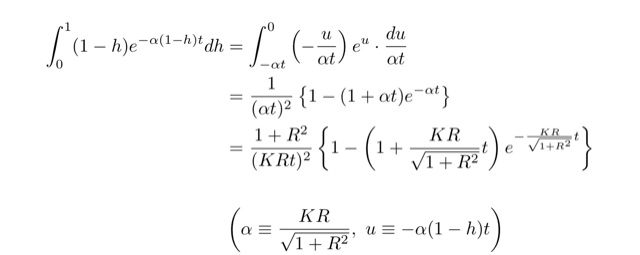
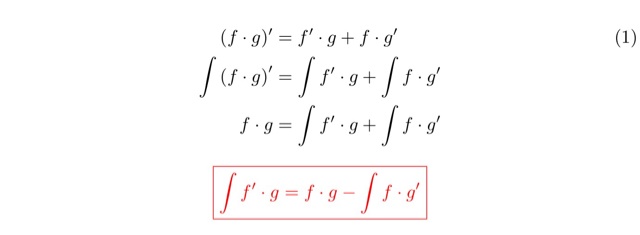
B:ビリヤード台の問題
速度が時間によって変化していくところが,少しひねっているところですね.どちらかというと,ポイントは「反射」をどう扱うかということだと思います.下図のように,反射する辺に対して対称な図形を考えることで,玉の軌跡が直線として表されます.

Bの後半(B-3, B-4)
(B-3)の「初速度vを十分大きくすれば」というのは,「無限大の初速度を与えた」ぐらいの解釈でいいと思います.物理的には変な表現になってしまいますが・・・
mが整数であることと高さが1(=m×1/m)であるということから,初速度が十分大きいとき,
- mが奇数であれば,点Bか点Cのいずれかに到達する.
- mが偶数であれば,点Oに戻ってくる「ループ」になってしまう.
ということがわかります.これが見抜ければ,後半の2問の山は越えたことになります.「玉がAまたはBに到達する」と条件が書かれていますが,実は点Aには到達することがない(点Bだけが考える対象になる)ことになります.
(B-4)では,「移動距離」も考えなければいけません.点Bに到達するまでに,何回反射し,次の反射までに進む距離がどのようになるかを導きます.これは「折り返し」の図を用いた方がわかりやすいように思います.
1回目の反射以降は,次の反射までに進む距離が一定になっています.少し違った表現をすれば,1回目の反射以降では,次の反射までに高さ(AB方向の変位)が2/mずつ上がっていくということになります.

こうやって見てみると,Bの問題は微積を使うというよりは,整数問題の色が濃いようにも感じます(特に後半は).整数問題は具体例から推測をして,それが正しいことを論じるという流れが多いですよね.上の内容もそんな感じです.