蚊取り線香のうず巻き～その1～ - みをつくしのひとりよがり

先日，Eテレ2355金曜日の夜更かしワークショップで「蚊取り線香」を扱った内容が放送されていました．今回は，この内容を数学的に追っかけてみます．

元ネタ

夜更かしワークショップでは，「蚊取り線香のうず巻きの中間地点は，どのあたりなのか？」という問いでした．中間地点とは，うず巻きに沿った長さに対する真ん中という意味になります．放送では，外側の端とうず巻きの中心(これも端ですね)の両方に火をつけ，燃えていった先がぶつかるところとして求めていました*1．見た感じでは，外側の端から角度でいうと1周とちょっとのところが中間地点となっていました．
これを定量的に(計算で)求めてみたいと思います．

蚊取り線香のモデル化

うず巻きをもっともらしい図形に置き換えます．それは「アルキメデスの螺旋」と呼ばれるものです．この関数は，式の形が非常に簡単なものです．極座標表示とパラメータ表示で，それぞれ以下のように表されます．
f:id:miwotukusi:20150729235905p:plain

一般には， $r=a \theta$ ( $a$ は定数)と書かれますが，ここでは $a=1$ として考えていきます．さらに，うず巻きは「4周」( $0 \leq \theta \leq 8 \pi$ )しているものとします．イメージは下図のようになります．
f:id:miwotukusi:20150730005737p:plain

この図形の中間地点を求めることを考えていくわけですが，アルキメデスの螺旋で置き換えたことが間違っていれば当然違った結果が出てきます．以前にも書いていたように記憶してますが，このような議論をするときには，「何を前提(モデル化)として話を始めているのか」は忘れないように(振り返るように)して下さい．

うず巻きの全長を求める

まずは，中心から端までの長さを求めてみます．それは，角度の関数として与えられ，曲線の微小部分(線素)を積分することを考えます．パラメータ表示から線素を考えると，
f:id:miwotukusi:20150730001104p:plain

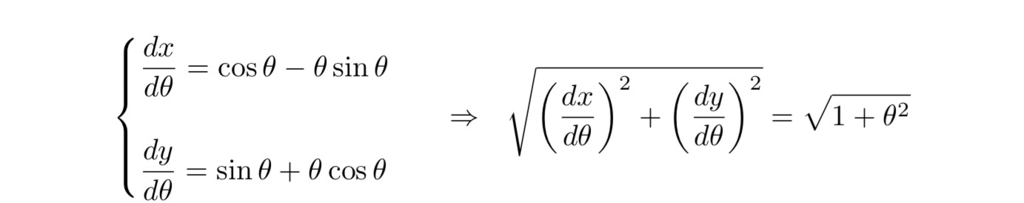
と求められます．意外とシンプルな形になりました．ですので，中心からの長さは
f:id:miwotukusi:20150730001206p:plain

という積分で与えられます．この積分，一見簡単そうですが，実はややこしいです．とはいえ，高校数学の範囲で計算ができるので，しばらくこの積分の計算を考えていきます．

積分計算

先に，この積分の結果(不定積分)を示してしまいます．
f:id:miwotukusi:20150730001418p:plain

積分計算は難しいのですが，答えが正しいかどうかは「計算結果を微分して，元に戻るか」で確認できます．また逆の計算をすることで，積分に対する経験値(どのような形になるかの目利き力)が高まると思います．

ポイントは，変数の置換の形です． $x+\sqrt{1+x^2} \equiv t$ と置きます．すると，
f:id:miwotukusi:20150730002221p:plain

となります．さらに，置いた式から
f:id:miwotukusi:20150730002420p:plain

も導くことができます．2乗の項が消えるところがポイントですね．さらに，(2式)を再度用いることで，
f:id:miwotukusi:20150730002652p:plain

と書き換えることもできます．
(1式)，(2式)をもとの式に代入して，
f:id:miwotukusi:20150730002826p:plain

第1項を因数分解して(2式)，(3式)を適用することで，最初に示した結果を導くことができます．

中間地点を求めるわけですが...

$L(\varphi)=L(8 \pi)/2$ となる $\varphi$ を求めるわけですが，導かれた式の形を見てもわかるように，普通に方程式としては求められそうにありません．ここは，数値解を関数電卓さんに求めてもらいましょう．
まず， $L(8 \pi)$ ≒318となります．そして，中間地点の $\varphi$ は約17.72と求められます．これはラジアン表記(弧度法)なので，度数法に置き換えると約1015度となります．外側の端からは，360度×4周 - 1015度 = 425度 = 360度 + 65度となり，「外側から1周と1/6周ほど進んだ点が中間地点」と求められました．Eテレの内容と，まあ合っているのではないかなと思います．
f:id:miwotukusi:20150730010124p:plain

蚊取り線香は，アルキメデスの螺旋とみてよさそうですね．ひとまず，目的は達せられた感じです．しかし，もうちょっと突っ込んでみると，いろいろと疑問が湧いてきます．というか，湧いてきてますか？(笑)
次回は，その湧いてきた疑問などをもうちょっと掘り下げてみたいと思います．

*1:実際には，うずの位置によって燃え方が異なるようです