前回の続きです.本題に入っていきます.
ヒートポンプ
先に挙げたカルノーサイクルは,P-V図において時計回りにその過程が進んでいきました.これを反時計回りに進めることを考えると,
サイクルに仕事を「与え」,低温部から高温部へ「熱を移す」
というサイクルになります.このような装置を「ヒートポンプ」と呼びます.
最近の空調機器や乾燥機といったものには,たいていこのヒートポンプが用いられています.関西のガス会社は「ガスヒーポン」という商品を出していますが,この「ヒーポン」がヒートポンプのことを表しています.
低温部から高温部に熱を移すというのは,一見ムダに見えます.いまの時期であれば,外の冷たい空気から熱を移してきても冷たいだけやん!と思われるかもしれません.以下では,それがムダではないことを記していきます.
サイクルの「効率」を定義する
サイクルの向きによって,その効率に対する考え方(定義)が変わってきます.
- 熱機関(高温部から力学的エネルギーを取り出す機関):高温部から取り出した熱のうち,どれだけを仕事に回すことができたか(熱効率)
- ヒートポンプ(低温部から熱を吸い上げ高温部へ移動させる装置):与えた仕事に対して,どれだけの熱を高温部へ取り込むことができたか(成績係数)
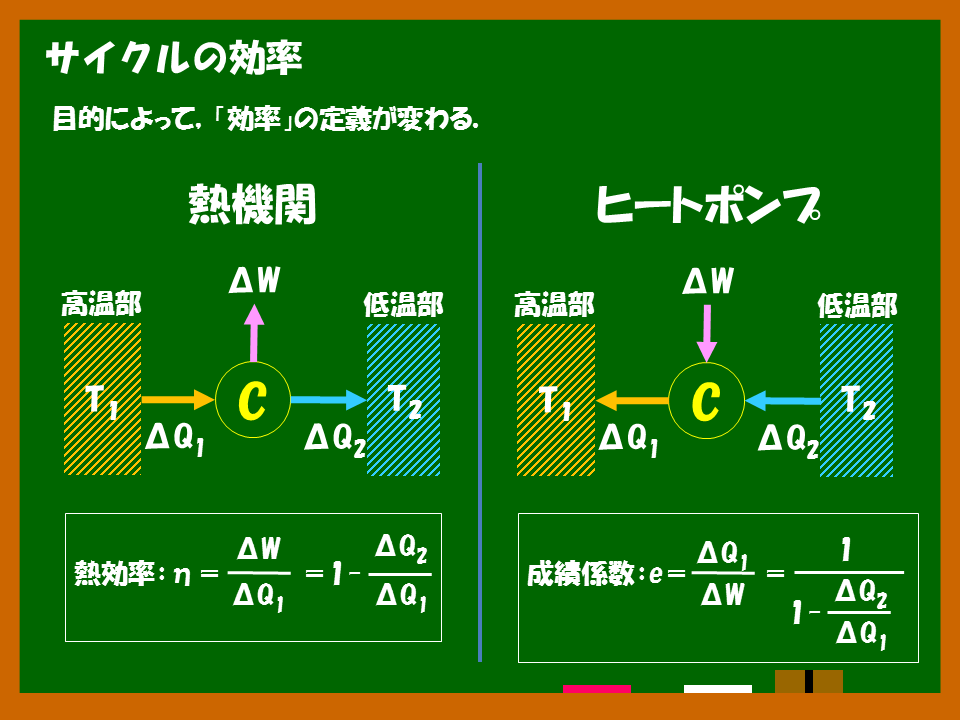
熱効率@熱機関
高温部から熱量:を取り出しサイクルへ熱を送る.このサイクルから取り出した仕事の量(力学的エネルギーの量)を
,このサイクルから低温部へ流す熱量を
とするとき,熱効率:
*1は,以下の式で与えられる.
また,である.
成績係数@ヒートポンプ
低温部から熱量:を吸い出し,仕事:
を与えられたサイクルを通じて
の熱を高温部へ移す.このときの効率を表す成績係数:
は,以下の式で与えられる.
ですから,この係数は 1よりも大きな値となります.
必要な仕事を計算してみる
だけの熱量を取り入れたり,取り出したりするのに必要となる仕事:
がどのくらいになるかを考えてみます.

ヒーターの場合
このとき,成績係数の式は,
となり,必要な仕事は と与えられます.
もし,室内に電熱器を置いて同じ熱量を得ようとすると,無駄がなかったとしても だけの仕事をしなければなりません.明らかに,ヒートポンプの方が効率がよいことがわかります.
クーラーの場合
同様に,成績係数の式を立ててみると,
より,となります.こちらは,単純に
であるとは言い切れません.また,クーラーの方がヒーターよりも無駄な感じ(
)になっています.
一番効率のいい場合で具体例を考えてみると...
上の計算では,クーラーの場合がヒーターの場合に比べて,無駄なのかどうかよくわらかなくなってしまいました.そこで,具体的な数値を使って考えてみます.その例として一番効率のいい場合を考えてみます.
これは,(逆)カルノーサイクルの場合となり,熱量の比は熱源の温度の比になっています.つまり,成績係数は温度の比より計算されることになります.そもそも,実際の装置でも,暖房(ヒーター)と冷房(クーラー)で同じ成績係数というわけではありません.
たとえば,
- ウォームビズの場合,推奨されている室内の温度は 20[℃]
- クールビズの場合、推奨されている室内の温度は 28[℃]
であり,これと
- 大阪の2016年1月の日最低気温の平均=3.4[℃]
- 大阪の2016年8月の日最高気温の平均=35.0[℃]
を外気の温度として必要な仕事を考えてみます.*2
まず,成績係数を熱源の温度を用いて書き改めると,
となります.(高温部の温度)÷(内外の温度差)という値になっています.
あとは,それぞれの場合に対して,を当てはめるだけです.すると,
- ウォームビズのとき,
- クールビズのとき,
となります.両者の式は(内外の温度差)÷(室内の温度)×(移したい熱量)という式になっているので,温度差が大きいと効率は悪くなるということになります.*3結果,同じ熱量を移す場合には,ヒーターの方が大きなエネルギー(仕事)を要することになります.
クールビズの方が服装の変わり様が大きいので,そちらばかりが注目されてますが,ほんとうはウォームビズの方が大事だということです.ただ,暑いときも寒いときも無理は禁物なので,ほどほどに.