ドップラー効果～その1：公式の導出～ - みをつくしのひとりよがり

前回のキャッチボールの話のつづきです．次は，ボールの代わりに「音波」を投げ(？)ます．前回と同様に「時間間隔が変わる」話をして，その結果ドップラー効果が現れることを示します．まあ，教科書の復習のようなものです．

Pさんをスピーカーに変えました．(Pさんに決まった音階で叫んでもらうという手もありますが)
考えるケースも前回と同じです．

ケース1：近づきながら音を出す

図は以下のようになります。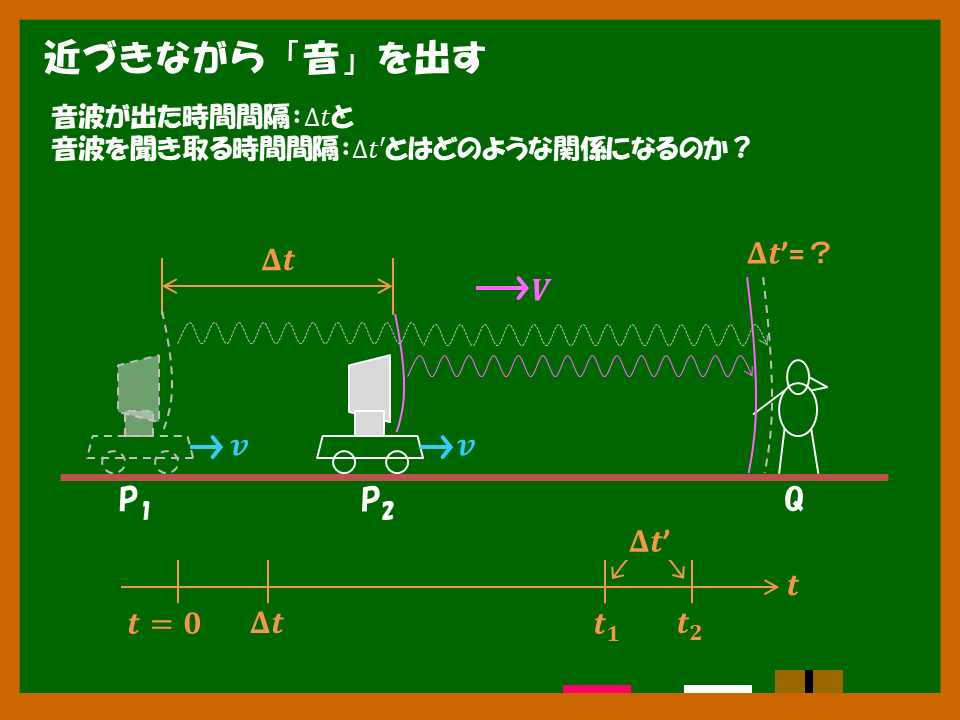

各点間の距離は，以下のようになります．

$P_1Q = V \cdot t_1$
$P_1P_2 = v \cdot \Delta t$
$P_2Q = V \cdot (t_2 - \Delta t)$

そして，距離の関係より
　 $\begin{align} V \cdot t_1 &= v \cdot \Delta t + V \cdot (t_2 - \Delta t) \\ -V \cdot (t_2 - t_1) &= (v - V) \cdot \Delta t \\ t_2 - t_1 &= \frac{V-v}{V} \cdot \Delta t \end{align}$

$\displaystyle{ \Delta t’ = \frac{V-v}{v} \cdot \Delta t}$ という関係が得られました．ここで，スピーカーから出す音波の周波数を $f$ ，Qさんが聞く音波の周波数を $f’$ します．(周波数)×(時間)は，その時間内の波数を表しています．時間： $\Delta t$ の間に出た波は，そのままの波数で時間： $\Delta t’$ の間で届くので，
　 $\begin{align} f’ \Delta t’ &= f \cdot \Delta t \\ f’ \left\{ \frac{V-v}{V} \cdot \Delta t \right\} &= f \cdot \Delta t \\ f’ &= \frac{V}{V-v} f \end{align}$

という関係式が導かれます．これが音源が動く場合のドップラー効果の式になります．
引き続き，ケース2もやってしまいます．

ケース2：走りながら音を聞く

これも図を出しておきます．

各点間の距離は，以下のとおり．

$PQ_1 = V \cdot t_1$
$Q_1Q_2 = u \cdot (t_2 - t_1)$
$PQ_2 = V \cdot (t_2 - \Delta t)$

これらは，前回の Qさんが動いたときと同じ式になっています．ですので，結果も同じで
　 $\displaystyle{ \Delta t’ = \frac{V}{V-u} \cdot \Delta t }$

となります．さらに，先ほど同様にこれらの時間間隔での波数が同じであることから，
　 $\begin{align} f’ \cdot \Delta t’ &= f \cdot \Delta t \\ f’ \left\{ \frac{V}{V-u} \cdot \Delta t \right\} &= f \cdot \Delta t \\ f’ &= \frac{V-u}{V} f \end{align}$

という観測者が動く場合のドップラー効果の式が得られます．

ケース3：両者が動く場合

スピーカー：Pと Qさんの間に「動かない」Rさんを仲介者として置き，

動かない観測者として，音波を受け，
動かない音源として，音波を出す．

という役回りをしてもらうことで，
　 $\displaystyle{ \Delta t’ = \frac{V-v}{V-u} \Delta t }$

となり，結果
　 $\displaystyle{ f’ = \frac{V-u}{V-v} f }$

という一般的なドップラー効果の公式を得ることができました．わたしが習ったときには音源；Source，観測者；Observerの速さをそれぞれ $v_S, \ v_O$ と表して，
　 $\displaystyle{ f’ = \frac{V-v_O}{V-v_S} f }$

と書いて，「観測者：Observerは Overで上(分子)，音源：Sourceは Shita(下)で分母」と覚え方を教わりました．(英語と日本語が混在ですが...)

と一気に公式まで書き下しましたが，前回との違いに気づいたでしょうか？
ケース1における式の形が違っています．これは，スピーカーから出た音波の速度が $V+v$ (相対速度)ではなく， $V$ であることによるものです．音波はあくまでも媒質(空気)の振動により伝播するので，媒質の移動がなければ音速は $V$ のままになるというわけです．
そして，同じ波数を異なる時間間隔で受けることとなり，それが周波数の違いとなって聞こえるという現象を与えることとなるわけです．

次回はドップラー効果の具体的な問題を挙げてみます．