「2022年京大物理第2問」のメモ - みをつくしのひとりよがり

京大さん第2問は，いつもどおりの電磁気の問題です．といっても，「無限はしご回路」が出てくるので，一度問題に当たっていないと難しいのかもしれません．あと，この大問は(1)〜(5)までの場面転換があるので，話がコロコロと変わっていくという点でも時間が足りない難しい問題かもしれません．

問題の中でも出てきますが，「棒磁石が動くこと(はしご導体は固定)」と「はしご導体が動くこと(棒磁石は固定)」は同じとみなすことができます．固定された磁界中を導体棒が動くというのが定番なので，上のように考えて置き直す手もあるにはあります．

(1) 無限はしご回路を「置き換えて」考える．

磁界の変化がともなわない部分(左側と右側)を1つの抵抗に置き換えた等価回路を考えます．

[イ] 誘導起電力
単位時間あたりに棒磁石は $v$ だけ動くので，閉回路における単位時間あたりの磁束の変化は $B a v$ となります．向きですが，棒磁石による磁界は，無限はしご回路の下から上の向き(問題紙面の裏から表の向き)になっているので，磁界が上から下に向くような電流の向きを考えればよいことになります．結果，図2(b)(または(c))の矢印の向きのままに流れます．

[ロ] QからPに流れる電流
一度，回路図を書き換える(等価回路というよりは，抵抗のつながり方の見方を変える*1ようなことをしてみてもいいと思います．似ているイメージとしては，2020年センター試験物理のメモ - 理系男子の独り善がりの第2問Bに描いている図のような感じです．こうすると，半無限部分が並列つなぎになっているイメージがつかめると思います．この並列つなぎになっている部分の合成抵抗は， $\displaystyle{ \frac{1}{R'} = \frac{1}{R_{\infty}} + \frac{1}{R_{\infty}} }$ より $\displaystyle{ R' = \frac{R_{\infty}}{2} }$ と求められるので，流れる電流の大きさ： $I$ はキルヒホッフの第2法則より，以下の式から求められます．
　 $\displaystyle{ I \left( R + \frac{R_{\infty}}{2} \right) = B a v }$

[ハ] 棒磁石を動かすために必要な仕事
単位時間あたりの仕事なので，仕事率を求めることになります．これは，回路の消費電力で失われるエネルギーをおぎなうことを考えます．よって，必要な仕事は $I \cdot B a v$ より求められます．

(2) 無限はしご回路の抵抗値

ここができないと後が続かないところですね．(1)でも半無限部分を1つの抵抗に置き換えるということをしているので，それを真似ればいいです．

問1 無限はしご回路の抵抗値

図3(b)にあるように，PQから左を丸々 $R_{\infty}$ とした回路と
KLから左を $R_{\infty}$ とした回路

の抵抗値が等しいとして考えます．注意点としては，「 $R_2$ の抵抗をどこまで含めるか」です．
立てられる式( $R_1$ と $R_2$ の比を代入する前)は，次のようになります．
　 $\displaystyle{ R_{\infty} = 2 R_2 + \frac{R_1 R_{\infty}}{R_1 + R_{\infty}} }$

抵抗の比を代入すれば， $R_{\infty} = R_1$ が導かれます．

ここの考え方ですが，たまに数学のクイズとして出てくる
「 $\sqrt{ 2 + \sqrt{ 2+ \sqrt{ 2+ \sqrt{\cdots}}}}$ の値は？」
の考え方に似ていると思います*2．

(3) 回路を流れる電流

[ニ] QからPに流れる電流リターンズ
[ロ]のところで求めた電流を $R$ と $E$ を用いて表します．
　　 $\displaystyle{ I_0 \left( R + \frac{R}{2} \right) = E }$

[ホ]～[ヘ] 回路を流れる電流
『(2)で述べたことを利用すれば』と書かれているので，(2)で用いた等価回路を用いて考えます．

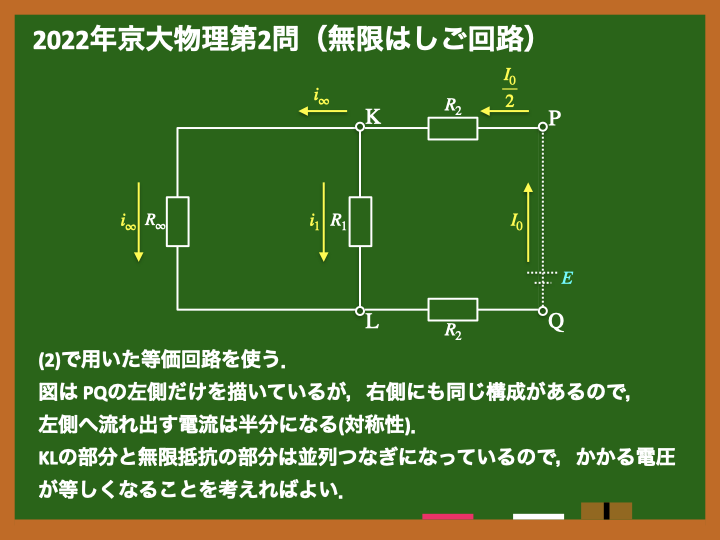
f:id:miwotukusi:20220408185952p:plain:w500 — 等価回路

図からは[ホ]が求まりますが，同様にして(1つ左にずらして考えれば)[ヘ]を求めることができます．ちょうど半分ずつに分けられていくイメージですね．

(4) 厄介な発光ダイオードが登場

この発光ダイオードの電流電圧特性が，なかなかの厄介者です．図5(b)にあるように，この発光ダイオードにかかる電圧(順方向電圧)が $V_d$ 以上のときは，電流が無限大になるのですが，このときに，発光ダイオードには $V_d$ の電圧がかかっていることがポイントになります．ちょっと読み取りづらいですね...
あとは，先の2)(3)と同様に，半無限回路を含めた等価回路を考えればよいことになります．これらの半無限回路と発光ダイオードは並列つなぎになっています．

[ト] 発光ダイオードに電流が流れる条件
発光ダイオードに電流が流れるまでの間において，発光ダイオードにかかる電圧はPQ間にかかる電圧に等しく $E - I_0 R$ ( $I_0$ は[ニ]のときのもの)となる．この電圧が $V_d$ に等しいことが条件となります．

[チ]〜[ヌ] 各部に流れる電流
[ト]の条件をクリアすると，発光ダイオードにおいて $V_d$ の電圧降下が生じます．Q→P→発光ダイオード→Qの閉回路におけるキルヒホッフの第2法則を考えると，
　 $E = I_0 R + V_d$

この $I_0$ が2つの半無限回路と発光ダイオードの回路に分岐していくので，キルヒホッフの第1法則より発光ダイオードに流れる電流を $I_d$ とおくと，

PKの部分を流れる電流は $\displaystyle{ \frac{I_0 - I_d}{2} }$ となり，(3)の考え方を使えば $\displaystyle{ i_1 = \frac{I_0 - I_d}{4} }$
閉回路QPKLにおけるキルヒホッフ第2法則を適用すると， $\displaystyle{ E = I_0 R + 2 \times \frac{I_0 - I_d}{4} \frac{R}{4} + i_1 R}$

これらを連立させて， $i_1, \ I_d$ を求めます．

(5) 長い棒磁石の場合

長さが3倍になる棒磁石が動いた場合を考えます．問題文にある『(3)の結果を3つ重ね合わせることで容易に求めることができる．』を利用します．「重ね合わせ」という言葉ですが，物理においては「それぞれ独立しているものを足し合わせる」というイメージになると思います．(3)の図4のように，1つの場合には棒磁石がまたがっている縦の部分(PQ)に $I_0$ が流れているので，同様に K'K，PQ，KLのそれぞれに $I_0$ が流れるとして足し合わせていきます．
例として，PQについて書いてみると[ニ]で求めた電流を $I$ とおいて，

左側1つ分の棒磁石から $\displaystyle{ -\frac{1}{4} I }$ (P→Qの向きに流れるので負)
真ん中1つ分の棒磁石から $I$
右側1つ分の棒磁石から $\displaystyle{ -\frac{1}{4} I }$ (P→Qの向きに流れるので負)]

よって， $\displaystyle{ I_0 = - \frac{I}{4} + I + \left( - \frac{I}{4} \right) = \frac{I}{2} }$ となります．[ル]
同様にして，[ヲ]は $\displaystyle{ -\frac{3}{8} I }$ ，[ワ]は $\displaystyle{ \frac{7}{16} I }$ と求まります． $I$ の値を代入して答えを書かないといけないので，そこも注意です．
図に書き込むのであれば．3色ペンで色分けして書き込みたいところです．

問題のポイントは冒頭に書いている内容になりますが，地味にこの問題のいやらしいところは，(3)以降において，電流を同じ $I_0, \ i_1, \ i_2$ を用いて書いているところかなと．無限はしご回路自体はパズル的な要素もあって，面白いとは思います．

*1:トポロジー的な考え方ですね．

*2:求める値を $x$ とおくと， $x = \sqrt{ 2 + \color{red}{\sqrt{ 2+ \sqrt{ 2+ \sqrt{\cdots}}}}} = \sqrt{ 2 + \color{red}{x}}$ と与えることができ，両辺を2乗して得られる2次方程式を解いて， $x = 2 \ (x > 0)$ となる．