前回までの内容をまとめてみると,次のようになります.
ここまでくると,次の内容はさほど難しい内容ではなくなってきます.
7.不動直線と不動点
不動直線はすでに先の内容で与えられています.原点を通り,固有ベクトルを方向ベクトルとする直線が不動直線になります.さらに,固有値が1となるものは,向きだけでなく,大きさも変わらないので,不動点の集まり(不動直線の特別バージョン)として与えられます.
もしも固有値が0だったら・・・
「固有値が1」の特別バージョンがあるのなら,0の場合も考えたくなりますよね??(笑)
まず固有値が0となるときには,行列がどのような形になるのかを考えてみます.
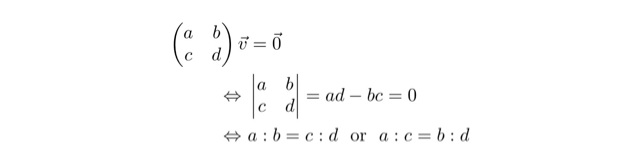
行列の成分に比の関係があることがわかりました.固有方程式の形を考えた方がわかりやすいのかもしれませんね.この結果をもう少し具体的な表現にして表してみると,行列Aは
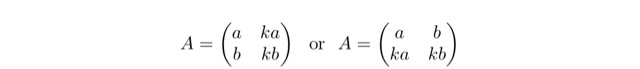
のように与えられることになります.細かい計算は省きますが,どちらの場合も固有値はλ=0,a+kbと与えられます.それぞれの固有値に対する固有ベクトルをv0→,vk→とすると,平面上の任意の点について,
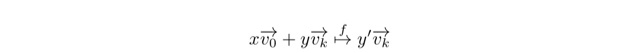
となり,すべての点がvk→で与えられる直線上に移されることになります.わたしの中では「平面をつぶす変換」と呼んでいます.
さて,この行列Aについてn乗を求めようとすると,対角化することができません.ちょっと計算してみれば,n乗の形は容易に推測ができます.ここはご自身で計算してみてください.
8.1次変換の使い道
物理で重要と書きましたが,物理では固有ベクトルを「固有状態」という言葉で扱います.
たとえば,座標平面のx軸とy軸をそれぞれ位置と速度に対応させて,物体の運動を表すと考えたりします.運動の「本質」(外力など)を行列で表すことができれば,物体の運動を座標平面上の軌跡として考えることができるようになります.さらに,その座標平面上の点を固有ベクトルを用いて表しておけば,運動しても軸がブレないようになり表現がしやすくなるということになります.
というわけですが,実際に勉強したことがないと,この感覚はつかみづらいように思います.上の例もだいぶ苦しいですし・・・.
大学で勉強するような物理というと,微分積分ばかりなイメージがあるかもしれませんが,行列表現もよく使うものです.慣れ親しんでおいてくださいね.
最後に,このシリーズでいろいろと計算過程を挙げていますが,上の「固有値が0の場合」のように,いろいろと場合分けしなければならないようなところを飛ばしている箇所があります.なるだけ,感覚的にしようとした結果です.気になる人は,とことん突き詰めてみてください.