※すみません,2018/01/11にタイトルを修正しています.(“縦波の反射”←”縦波の反射波”)
2024/11/03改修
最近,このネタを比較的よく見ていただいているようです.ありがとうございます.
久しぶりに読み返していたのですが気になったところがあったので,追記する形で改修をします.
2018/01/13 大事な追記
スッキリできるやっぱりできない説明が本家から出てきました.
理科問題(物理) 〔3〕Aの解説(1月12日追記)
「壁での反射」がどうこうという話ではなく,「音叉から出る音」に違いがあったようです.そして,これは問1にも絡む内容だったようです.というわけで,以下の解釈は違うということになってしまいました.しかし,位相と疎密(音圧)の違いを改めて認識できたことは収穫だったのかな?と思っています.
ところで,音叉から出る音波の位相が定かでなかったとすると,「3つの正解をとる」よりも問題自体を不適とする方が正しいような気もしていますが.
2018/02/01追記:解説に書かれている内容について,少しメモを書いているので参考にしていただければ幸いです.
2018/02/01追記:京都大も結局...
ごちゃごちゃしてしまいますが,内容的にはかぶっているのでココに追記します.
下の元ネタでも少し触れていますが,2017年京都大物理 III (4)も指摘を受けることになりました.
https://www.asahi.com/articles/ASL2153XGL21PLZB00W.html
こちらは音叉ではないので,やはり反射のところ(注釈にチラッと書いていました)なのでしょうか?また,公式発表があるかとは思っていますが.
2018/02/02追記:まとめてみました
わたしなりに今回の件についてまとめてみました.
miwotukusi.hatenablog.jp
(以下,2018/01/15の元ネタです)
新年早々ニュースになった大阪大物理の問題を発端としたネタです.
大阪大採点ミス:外部からの指摘、3度目で認める | 毎日新聞
TVのニュースでチラッと問題を見たときは,「ああ,ドップラー効果の問題か.でも,どこ間違えたのかな?」と思っていました.でもその後,詳細に問題を見ていくうちに,いろいろと考えさせてくれる問題だったんだなということがわかりました.
いつものように備忘録メモを書いていきます.
波の話自体ひさしぶりなので,以下の順序で整理していきます.
- 横波の反射波
- 縦波の横波表示
- 音の観測とは?
- 縦波の反射波
- 2017年大阪大物理[3]の問題
1. 横波の反射波
ここは教科書どおりの話です.密媒質から疎媒質への反射か,疎媒質から密媒質への反射かによって,反射波の位相の様子が変わります.
- 密媒質から疎媒質への反射では,反射面は「自由端」となり,反射波の位相は変わらない.
- 疎媒質から密媒質への反射では,反射面は「固定端」となり,反射波の位相は反転する.

ざっくりした覚え方(言い方)をすると,
「やわらかいところから硬いところへ進んで反射するときは,位相反転する.」
という感じでしょうか?高校生のとき,「イソウハンテン」と聞いて,どこの中華料理屋さんのことかと思った記憶があります.
2. 縦波の横波表示
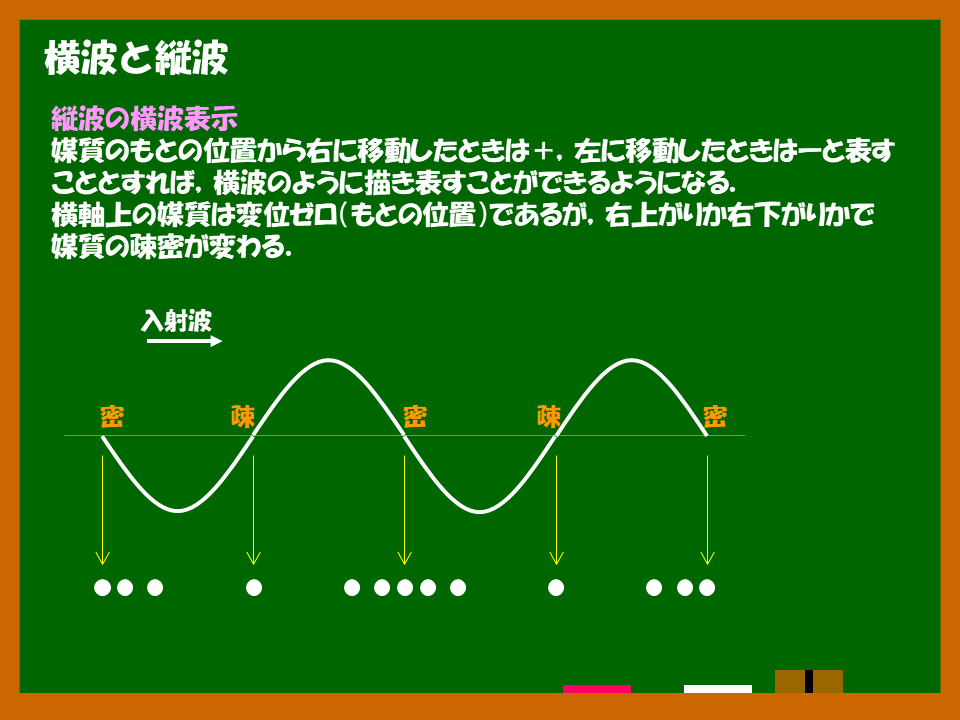
音波はご存知のとおり「縦波」または「疎密波」と呼ばれる波です.スリンキーというばねのおもちゃを用いれば視覚的にわかりやすいのですが,なかなか紙面上で表現するのは面倒です.そこで,媒質の変位を横波として表すことをします.「波の進行方向への変位を+とし反対方向への変位をーとする」などと書いたりしますが,ここでは入射波が右方向へ進行するものとして,「右方向への変位を+,左方向への変位をー」とします.位相が の中で変化するとき,
のときに変位の大きさは最大となりますが,もっとも疎や密となるのは位相が
のときとなっていて,両者にズレがあります.これが「ややこしや」の根源の一つになっています.
2024/11/03追記
ここは補足的な内容になります.図中「入射波」と言う表現が入っていますが,これを正の向きとしているわけではありません.図の上部にも記しているとおり,媒質が移動した向きについて,右向きを正としています.
3. 音の観測とは?
ここがひとつのポイントになります.後で大阪大の問題を出しますが,「音の強さ」を観測しています.つまり,変位をみているというよりは音圧(疎密)をみていることになります.ちょっと頭に入れておいてください.
4. 縦波の反射波
1.のときに描いた横波の反射波の絵を「縦波の横波表示」されたものとして見てみます.

すると,密な点(音圧が高い点)が入射して反射すると,
- 密媒質から疎媒質への反射では,密な点は疎な点(音圧が低い点)として反射する.音圧に関しては,固定端のような振る舞いをする.(表示を薄くした理由は下記追記にて)
- 疎媒質から密媒質への反射では,密な点は密な点(音圧が高い点)として反射する.音圧に関しては,自由端のような振る舞いをする.
1.で書いた固定端・自由端とは逆の振る舞いになっています.
改めて書き下すと,
- 横波でも縦波(横波表示されたもの)でも位相を考えたときは、自由端・固定端における振る舞いは同じであるが,
- 音圧で考えると,自由端・固定端の振る舞いは横波のときとは逆のイメージになっている.
ということになります.
2024/11/03追記
そもそも音波の反射って自由端なのか固定端なのかという話ですが,空気よりも疎(やわらかい)壁で反射ってなんか気持ち悪いというか,そもそも反射せずに透過するのでは?と思う方が自然かなと思っています.なので,このような自由端としての反射(図の上のケース)はあまり考えない方が良いのかと思っています.
また,音波(縦波)は「疎密波」であるという特徴を考えると,密(音圧が高い部分)で壁にあたった後,疎(音圧が低い部分)になって跳ね返るというのも不自然な話です.もう少し言い換えると,媒質が寄り集まっていた密の部分が,壁に当たっただけで媒質が散らばった疎の部分に化けるという手品のような話になるということです.このように考えれば,音波の反射は固定端反射であり,位相は反転しているが,疎密は変わらないということでスッキリできるかと思います.
5. 2017年大阪大物理[3]の問題
まずは「問題となった問題」を揚げておきます.(http://www.osaka-u.ac.jp/ja/news/topics/2018/01/06_01に揚げられている「公表資料」より抜粋)

「公表資料」に記載されている内容を追ってみます.
「問4」の訂正内容
正答とされたものは,以下の 3つとなりました.
- 当初の正答である
おそらく「壁が固定端となるか自由端となるのかが明示されていなかった」ので,いずれの場合でも正解にするということだと思われます.ちなみに,京都大でも同じような設問があり,そちらには「壁Mでの空気中の音波の反射条件は固定端反射とみなすものとする.」という記述がありました.*1
それぞれの正答は,以下の考え方により導かれます.
1.は固定端により位相反転されるので,経路差である が半波長の奇数倍となればよい.
2.と 3.は自由端により位相がずれないので,経路差が半波長の偶数倍(波長の整数倍)であればよい.この場合,音叉が壁にくっついている()の場合もありうるので,この点を考慮すると 3.も正答とみなされる.(
は 1からはじまる数とされているため.「音叉は壁に密着することはない」という条件も漏れていたことになる.)
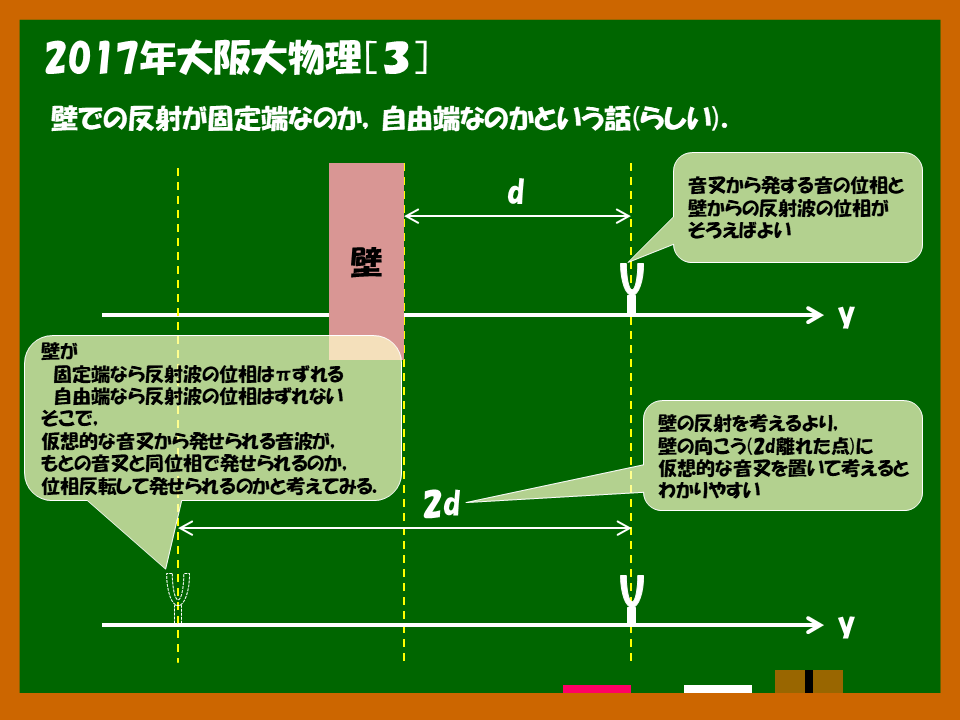
2018/01/12 図の補足:大阪大学が公表した解答(位相で考えた場合)に対する図.「位相」反転が起こる場合と起こらない場合で考えている.
「問5」の訂正内容
「問題の数値設定に不整合」と記載がありますが,これは上記問4の 2.と 3.を認めると,という観測域においては
という 3か所で観測ができてしまう*2ということによるものです.
ここでガツンとツッコミを入れてしまうと,上の 1.~ 4.で述べた内容を踏まえ,常識的に*3壁での反射は固定端であるとすれば「当初の正答」の方が間違いということになります.位相だけで考えるのではなく,さらに音圧(疎密の状態)まで考える必要があったという盲点を突かれたような問題だったことになります.そのうち,このような内容を論じさせる問題が出てくるのかもしれません.
2018/01/12追記:
こういう話は,うなりのときのように数式でさばくと結構スッキリすると思うのですが,ちょっと導入がないと問題にするには壁があるように思います.(正弦波であることが大前提となるところから)