しばらくぶりの更新です.前から書いておきたい(自分でも整理しておきたい)ネタを作っていました.それが1次変換です.
いつもは自分なりにひねったタイトルを考えるのですが,今回はストレートにしてみました.図形問題が絡むことが多いこともあり,高校のときは結構好きな分野でした.ただ,何をしたいのかがいまいちわからないまま,問題を解いていたという感じであったのは事実です.実は,大学で物理を勉強するには重要なウエイトを占めてくる分野なのです.ですので,大学で物理を勉強しようと思っている人は,行列・1次変換は慣れ親しんでおいて欲しいと思います*1.
ということで,慣れ親しんでもらえるかはわかりませんが,1次変換のことを何回かに分けて書いていきます.今回は先に見出しを挙げておきます.
書いているうちに,内容が脱線することもあるかもしれません.あしからず.
1.1次変換が変換してるものは?
高校数学の問題では「直線を直線に移す」というものが多いので,1次変換自体も図形を移すものという印象が強いですが,1次変換で見る基本の式をよく見れば,
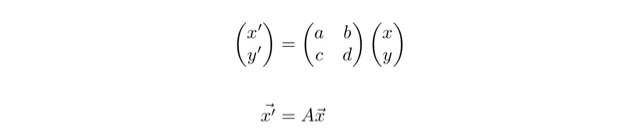
というように「点を点に移す」のが本質だということが理解できると思います.そもそも直線にしても,曲線にしてもグラフ自体点の集まりですよね.ある方程式を満たす点の集まりをプロットしたものがグラフなわけです.
これが理解できれば,円や線分といった範囲の限られている図形を変換したときにどうなるか(移された図形も範囲をもつ)ことも理解できると思います.

2.基本の変換いろいろ
単位行列は恒等変換.これは書くまでもないですね.他,基本的だなと思う変換を挙げてみます.
上から,拡大・縮小変換:S(a),x軸に関して対称移動:Mx,y軸に関して対称移動:My,回転変換:R(θ)の「四種盛り」になります.
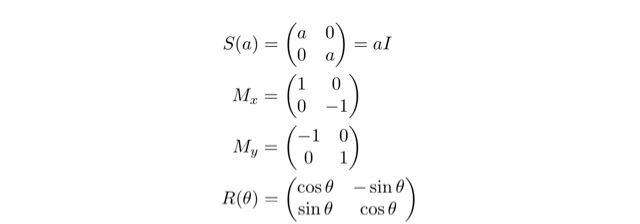
で,座標平面で基本的な変換(写像)として「平行移動」というのがありますよね.しかし,1次変換には平行移動は含まれていません.というよりも,表すことができないんです.原点を移すことを考えれば,無理だなあということがわかると思います.ちなみに,平行移動も含めた変換をアフィン変換と呼んだりします.*2
3.合成変換
試験でもよく出てくる合成変換を3つほど挙げておきます.
3-1.拡大・縮小変換+回転変換
これは「こういう形の行列は,拡大+回転を表していますよ」という例になります.変形の仕方は,三角関数の合成のときと同じイメージですね.
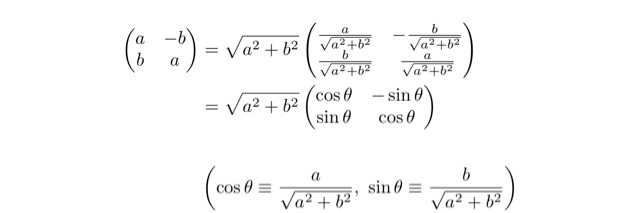
行列に√2や√3なんていう数字が入っているときは,この形になるかを確認してみてもいいかなと思います.
3-2.原点を通る傾き:θの直線に関して対称移動
これは基本変換の組合せとして表します.x軸に関して対称移動を使うことを考えていきます.
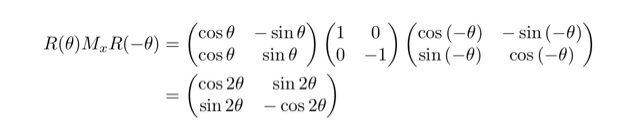
3-3.基本変換+基本変換を合わせても,基本変換
先に挙げた基本変換2つを組合せると,別の基本変換の一つになっています.中学数学風に言えば「原点に関する点対称移動」というやつです.
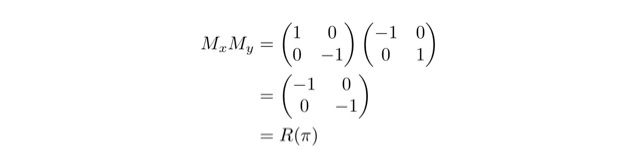
もうちょっと濃い内容をもった変換については,後ほどじっくりと.
4.可換と非可換について「書かん」とす
積の順番を変えても結果が変わらないものを可換,結果がかわるものを非可換と呼びます.行列はおなじみのように一般には非可換です.
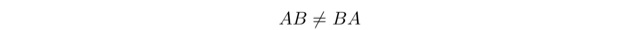
これを1次変換の世界で図形的に解釈してみると,「合成変換の順番が変わると,結果も変わる」ということになります.先に挙げた合成変換で考えてみると,
- 拡大・縮小変換+回転変換,x軸対称移動+y軸対称移動は可換であり,
- 傾き:θの直線に関して対称移動については非可換である
ことがわかります.つまり,行列の順番は勝手に変えてはいけない(結果が異なってしまう)ということです.
ひとまず,今回はここまで.